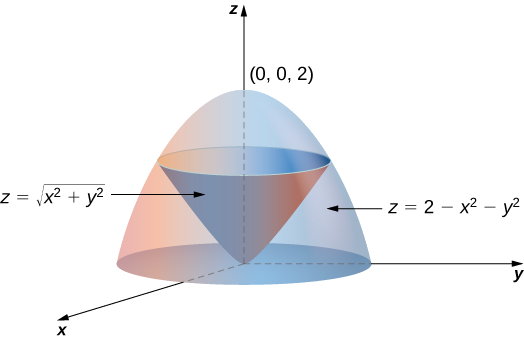
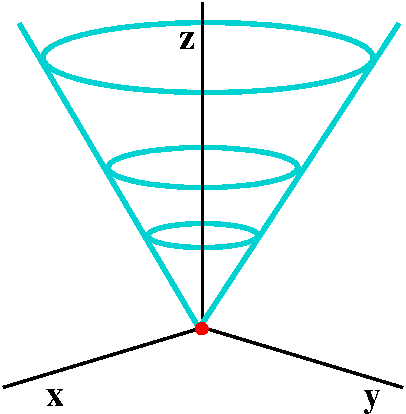
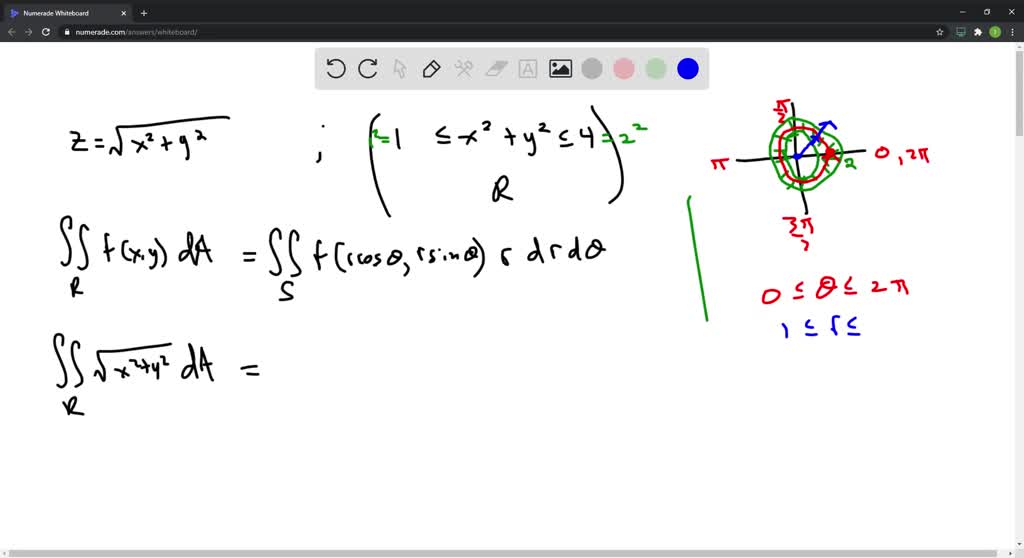
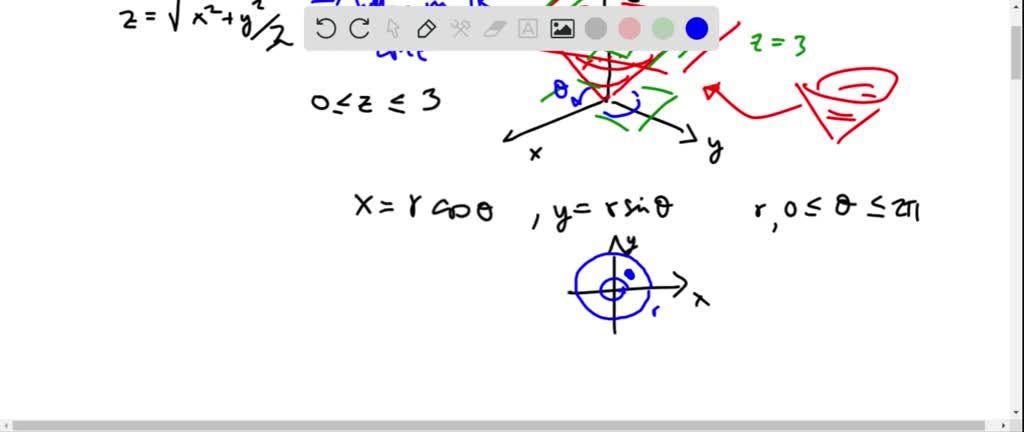
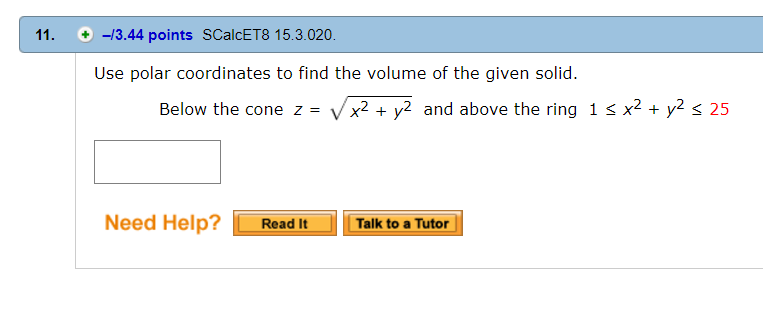
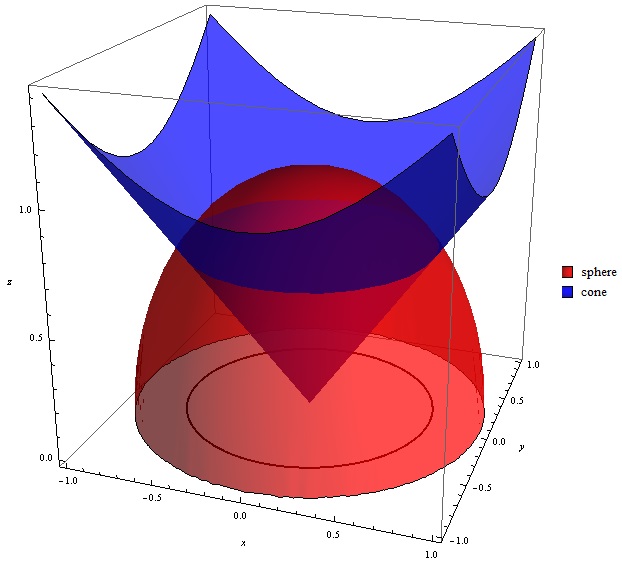
Problem Easy Difficulty Use polar coordinates to find the volume of the given solid Below the cone $ z = \sqrt{x^2 y^2} $ and above the ring $ 1 \le x^2 y^2 \le 4 $
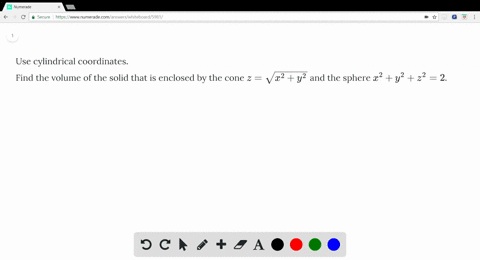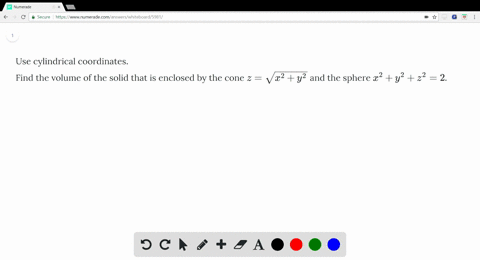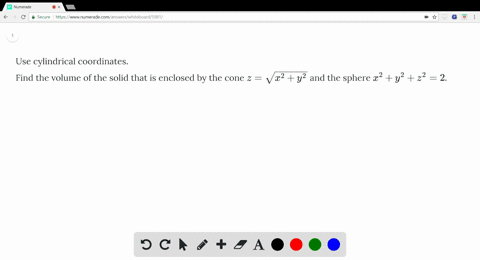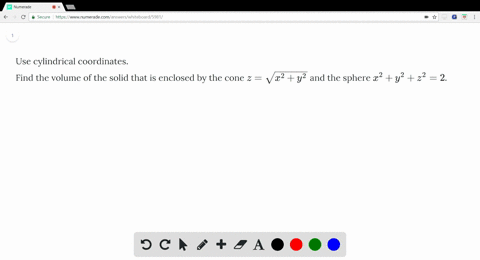
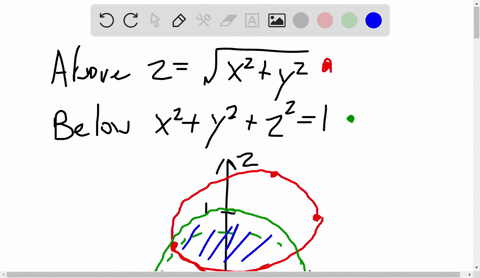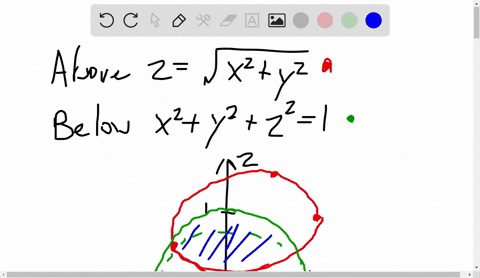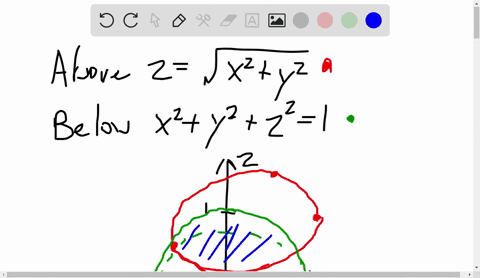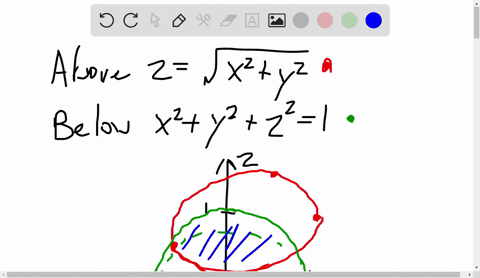
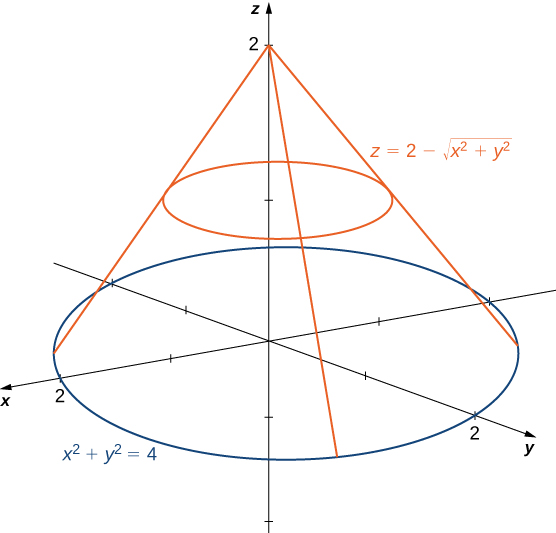
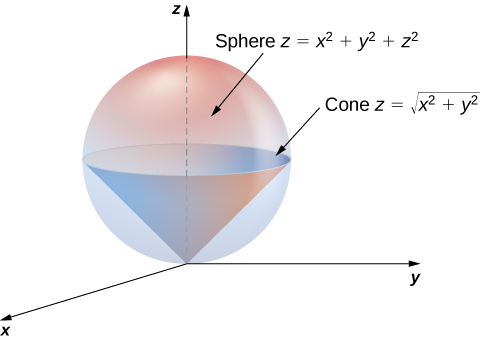
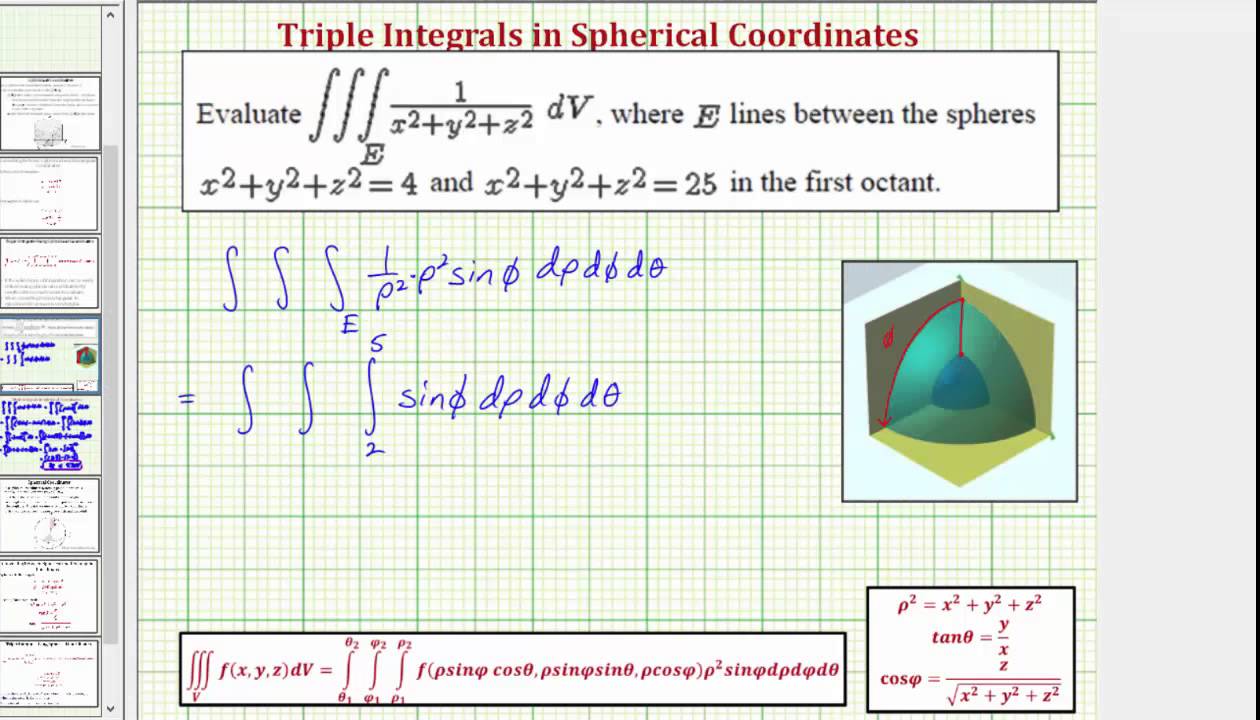
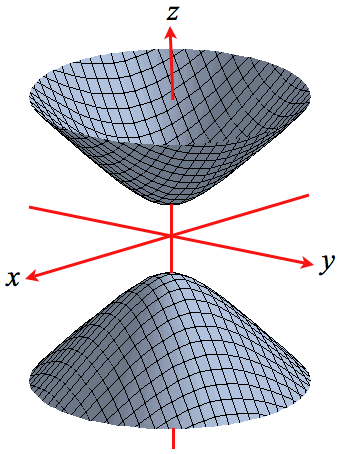
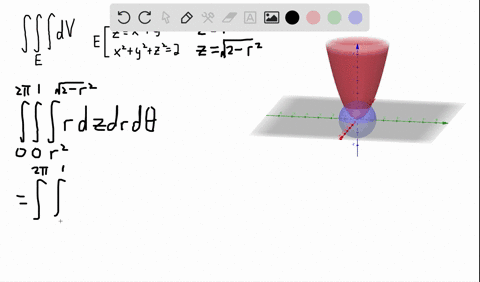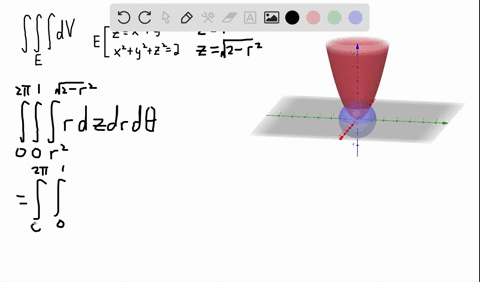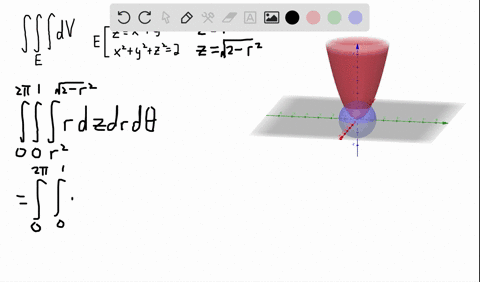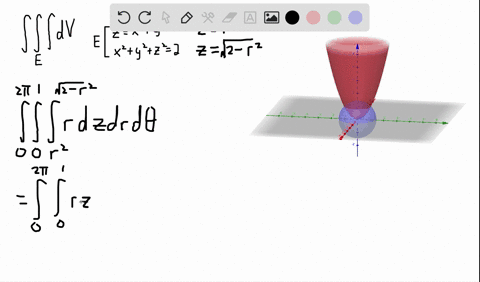
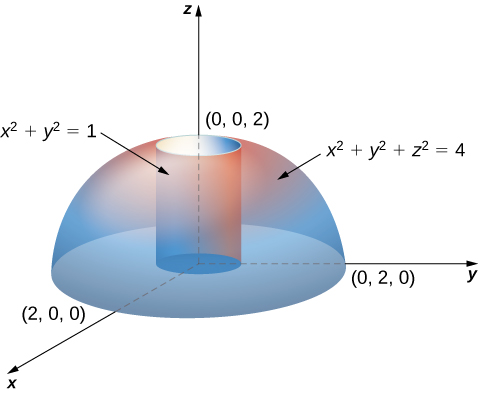
Z=sqrt(x^2 y^2) in polar coordinates-Problem 26 Medium Difficulty Use spherical coordinates Evaluate $ \iiint_E \sqrt{x^2 y^2 z^2}\ dV $, where $ E $ lies above the cone $ z = \sqrt{x^2 y^2} $ and between the spheres $ x^2 y^2 z^2 = 1 $ and $ x^2 y^2 z^2 = 4 $Last, in rectangular coordinates, elliptic cones are quadric surfaces and can be represented by equations of the form z 2 = x 2 a 2 y 2 b 2 z 2 = x 2 a 2 y 2 b 2 In this case, we could choose any of the three However, the equation for the surface is more complicated in rectangular coordinates than in the other two systems, so we might
Z=sqrt(x^2 y^2) in polar coordinatesのギャラリー
各画像をクリックすると、ダウンロードまたは拡大表示できます
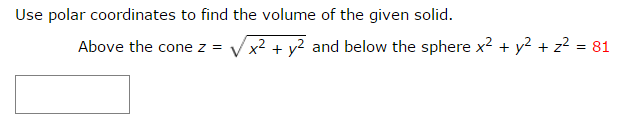 |  |  |
 |  |  |
 |  | |
 |  | |
「Z=sqrt(x^2 y^2) in polar coordinates」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  | |
 |  |  |
 |  | |
「Z=sqrt(x^2 y^2) in polar coordinates」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 | ||
 |  |  |
 |  |  |
「Z=sqrt(x^2 y^2) in polar coordinates」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  | |
 | ||
 |  |  |
「Z=sqrt(x^2 y^2) in polar coordinates」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  |  |
 |  | |
 | ||
「Z=sqrt(x^2 y^2) in polar coordinates」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  | |
 |  |  |
 | ||
「Z=sqrt(x^2 y^2) in polar coordinates」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  | |
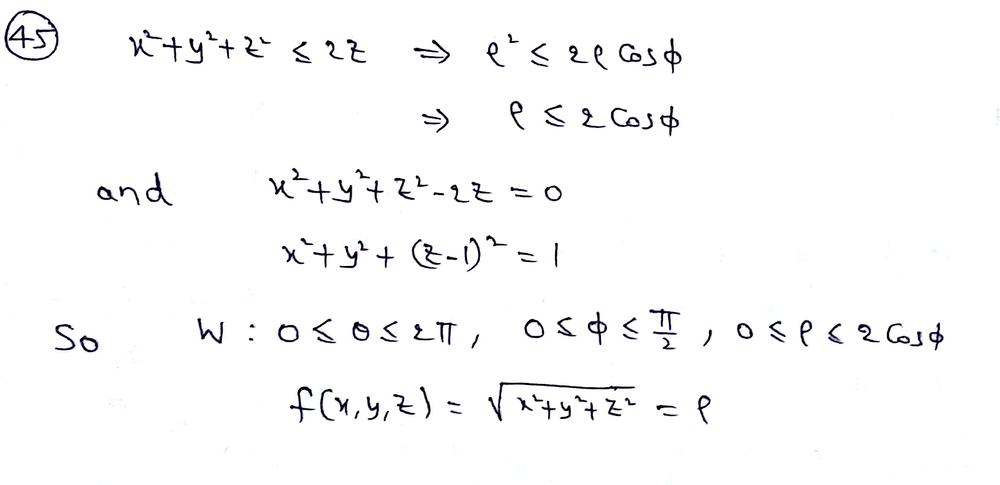 |  | |
 |  |  |
「Z=sqrt(x^2 y^2) in polar coordinates」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 | 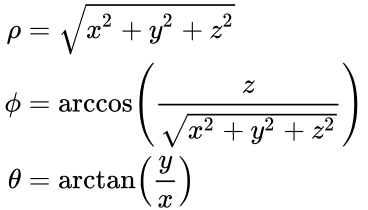 |  |
 | 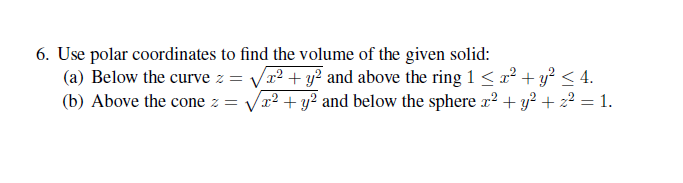 | 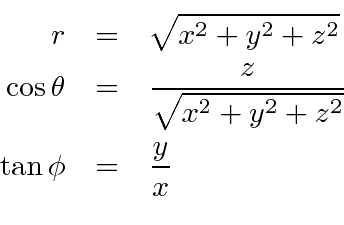 |
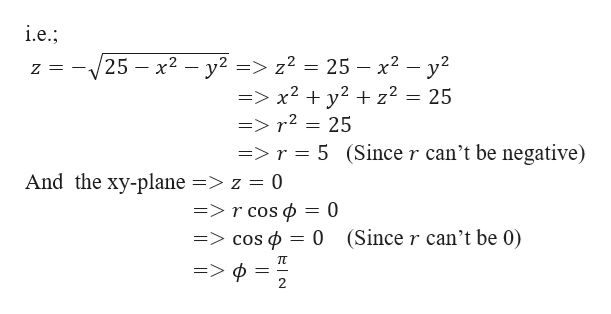 |  |  |
「Z=sqrt(x^2 y^2) in polar coordinates」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  |
\r=\sqrt{x^2y^2} \text{ and} \tan θ=\dfrac{y}{x}\ To sketch a polar curve from a given polar function, make a table of values and take advantage of periodic properties Use the conversion formulas to convert equations between rectangular and polar coordinatesAnswer to Using spherical coordinates, find the volume of the solid E that lies above the cone z = sqrt(x^2 y^2) and below the sphere x^2 y^2





0 件のコメント:
コメントを投稿